为什么采用渐进式估算尺

原文链接：http://www.yakyma.com/2012/05/why-progressive-estimation-scale-is-so.html

作者：Alex Yakyma

在本文中，我们将会讨论为什么渐进式的估算尺（Progressive Estimation Scale）——例如敏捷团队常用的斐波那契数列，比线性的估算尺更为有效，在为团队衡量backlog的故事的大小时，呈现更多信息。我们将会用到信息理论的一些基本原则来得到结论，同时，也会形成一个针对“归一化的估算基准”的假设。

在敏捷方法中，我们常常能看到大家使用“渐进式”估算尺对backlog的故事进行估算。最常见的方法是修正过的斐波那契数列：0, ½, 1, 2, 3, 5, 8, 13, 20, 40, 100。还有一种不太常见的估算尺，是XP（译注：极限编程）的拥护者们所倡导的：0, 1, 2, 4, 拆分 （本文中我们且将这种估算尺称为XP尺）。之所以称之为渐进式，就是为了说明，其价值的增长速度比线性增长更快。所以我们常常也会称这类估算尺（虽然通常情况下并不是100%准确）为指数式估算尺。

事实上，XP尺本身就是指数的，而斐波那契数列与函数 $f(x)=1.6^{x-1}$ 次方所定义的范围大致相当。参考下图：

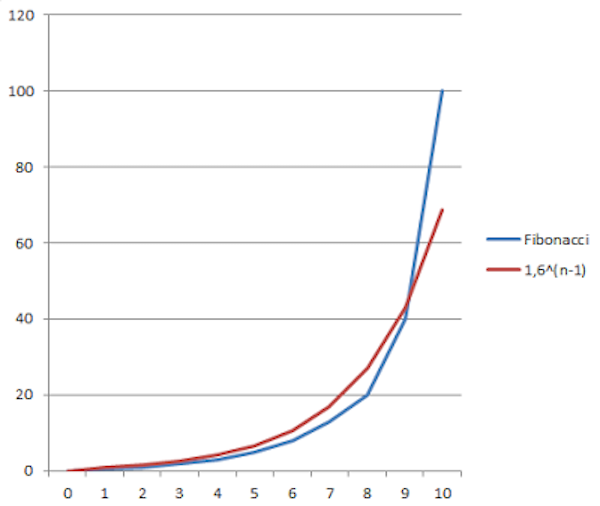
图1. 修正过的斐波那契数列的的数值范围与指数函数大致相当

在这里作此说明的目的，是为了表示这两种估算尺都具有同样程度的精确性，我们称之为“指数级”精确度。

话虽如此，还是让我们先反问自己：为什么要使用指数级的估算尺？众所周知，已经有成千上万的敏捷团队成功地应用了这类估算尺，是什么使得指数尺如此堪以大用？过去，我们面对此类问题，通常的回答是——提出backlog里的故事越大（比如N个故事点），那么说出N和N-1之间的差异就越难。这确实是正确的，然而这个回答本身并不是一个基本的公理，它只是基于一些通用原则的推论。就让我们来看一看这些原则。

信息理论视角

让我们换一个角度提出问题，假设我们（非常粗略地）知道backlog里故事U的大小不超过L个单位（可以是故事点，也可以是人·天，在这里这点并不重要），但是它可能是0到L的任意值，并且所有的可能性均等。假设，有一种估算技术，允许我们以P的绝对精确度估算出U的大小，那么我们可以看看，运用这种技术能得到多少关于故事U大小的信息。

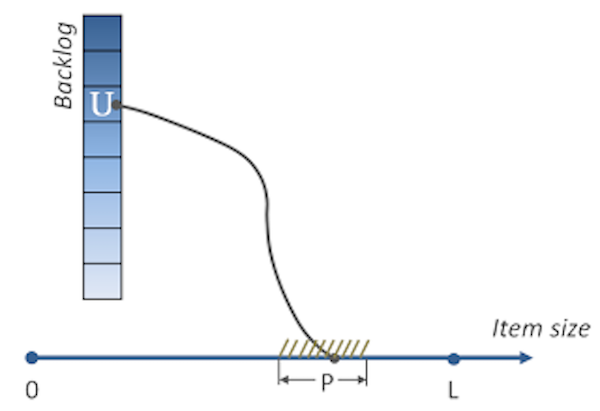
图2. 符号说明：U是backlog里的任意一张故事卡；L是backlog里所有卡片可能大小的最大值；P是估算的绝对精度；横轴上的连着U的点代表故事U的大小。

根据信息理论的基础知识我们知道，实验A中关于实验B的信息（也叫两个实验的互信息，详细可参考Wikipedia）可以表示如下：

$$I(A,B) = H(B) - H_A(B)$$

这里，$H(B)$ 是信息熵，也就是实验B的不确定程度。$H_A(B)$是实验A发生后，实验B的熵（也称为条件熵）。所以现在可以很容易将实验A中包含的的信息量解释为它为实验B所减少的不确定度。

现在，让我们把这个公式应用于我们的案例。我们也有两个“实验”，实验 (B) 是确定故事U的准确大小，实验 (A) 是应用我们的估算技术，从而在一定程度上减少不确定度（例如，获得一些信息）。避免展开数学深度的计算，这里我们仅需注意到，通过应用香农定律（实际上是互信息的一种定义），我们可以得到：

$$I(A,B) = log(L/P)$$

这里对数的底数并不是非常重要，它可以是符合对数简单特征（参考Wikipedia）的任意数量（大于1），但是通常人们会使用2作为底数，从计算机的角度来看，这倒是非常有意义，因为最终我们所有的信息都是以二进制形式存储的。

后面这个方程给出了一个非常有意思的结果：相比估算精度的提升，我们通过估算获得信息量的提升要慢得多。更具体地说，它是一个对数函数式的增长。通过下图这个对数函数图，我们就可以看出为什么“少量的估算事半功倍，而大量的估算事倍功半。”

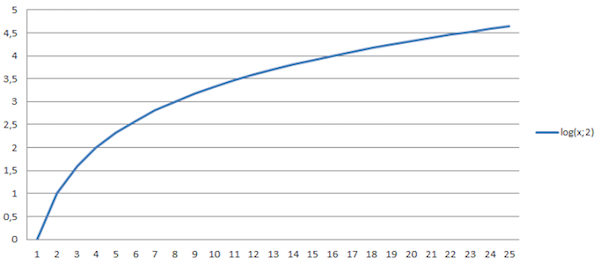
图3. 故事大小的信息的对数行为，可作为估算过程的结果。横轴代表相对精度（或者更精确的说，代表了(L/P)的值），纵轴代表信息量（以比特计）。

所以最终，使用指数（或近指数）估算尺就变得非常合乎逻辑了——有价值的信息增加得更快。确实，任意函数 $f(x)=a^{log_bx}$ 的增长肯定比 $log_bx$ 自身要快(a和b都大于1）。在理想环境下——现实中我们一定不会做此期待，当 $a=b$ 时，这个函数就变成了线性函数：$f(x) = x$。但是既然我们不会去声明这是必须的条件，那么我们通常就会说“信息增加得更快”，而不是“线性增加信息”。

归一化假设

另一个有趣的问题是，考虑到大多数团队都在使用斐波那契数列作为估算尺，他们是怎么确保他们“校正后的信息曲线”（例如，函数 $f(x)=a^{log_bx}$ 对应的曲线）能够增长得更快，从而使其比线性尺更加有用呢？显然，“信息曲线”的对数行为是可以肯定的，但是，如何在实际中找到确切的对数底数却不是件容易的事。虽说我们可以寄希望于团队通过自身经验能够找到斐波那契数列的正确用法，从而有效地获得信息。那么，什么是“正确用法”呢？

为了进一步简化分析（如前文所作的分析），我们可以使用某些指数函数，而不是斐波那契数列。即便底数是固定的（例如，$f(x)=a^x$ ），我们的团队还是可以改变函数本身，通过什么方式呢？对，正是“重新调节故事点”。确实，如果我们赋予故事点新的含义，比如说，以前的2个故事点等于现在的1个故事点，那我们的函数 $f(x)$ 变成了新的函数 $g(t)=f(2x)$ , 其中 $t=2x$ 。或者反过来，$x=0.5t$。如果我们替换掉前面公式中的$x$，我们可以得到 $g(t)=b^t$ ，其中 $b$ 是 $a$ 的平方根。新的函数 $g(t)$ 又成了一个指数函数，只是底数不同而已。下图这个例子，说明了重新调节故事点所产生的影响——如果我们将以前的3个故事点变为现在的2个故事点的大小，那么“估算尺曲线”会产生什么样的变化呢？

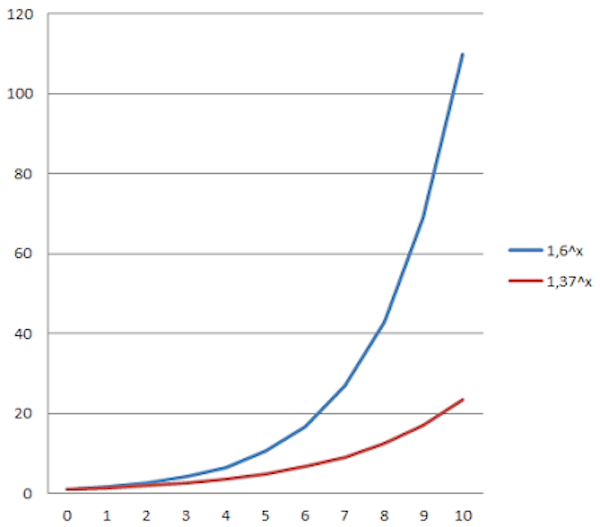
图4. 重新调节故事点——将原本的3个故事点变成新的2个故事点之后，指数函数（估算函数）的底数也随之改变。图中蓝线代表原来的估算尺，红线代表新的估算尺。

这就说明:

不断改变斐波那契数列的估算基础是一件非常有责任的事情，而这一点往往被低估。它可以让团队更趋高效的估算，当然，也有可能背道而驰。理想的估算底数只有一个，保证离它越来越近是很至关重要的。

现在，我们可以看看一个有趣的事实，也就是许多敏捷团队都可以确认的：

经过一段时间之后，敏捷团队常常会“归一”，到达一个近似于斐波那契数列的估算底数——在一个两周的sprint内，团队的平均速度通常为30-60个故事点。

当然，这也取决于团队规模，团队越小，这个数字越小；团队越大，数字也会越大。但也可能，这是团队为了更有效地管理潜在的可用信息，随着时间推移，不断优化其估算底数后的结果。基于此，我们也形成了我们的……

归一化假设：那些随着时间推移，使其估算基准归一化的团队，很大可能已经到达了他们的最佳估算能力（从他们估算过的，backlog里的项目所获得的信息的角度来看）。换言之，他们经验性的发现了这个指数函数，使得“矫正后的信息曲线”接近线性。

虽然看起来，要到达一个更好的估算基准，会有一段距离，但我们有了一个简单蠢笨但是可靠的方法作为开始。简单地在一个sprint给每个队员分配8个故事点，不是一个糟糕的初始估计值。事实上，考虑到上面的假设，当团队成员N从4到8变化时，我们得到的故事点$N×8$正好从32到64变化不等。

想要了解更多估算基准，可以参考 （Agile Software Requirements Enterprise Development 第八章，敏捷估算和速率）